GraphX内置图算法5：强连通组件

强连通组件（简称SCC）也是子图，其中所有顶点都连接到子图中的每个其他顶点（不一定是直接的）。SCC中的所有顶点都需要彼此可访问（沿着边的方向）。下图是一个带有四个强连通组件的图。与连通组件不同，SCC可以通过它们的一些顶点相互连接。

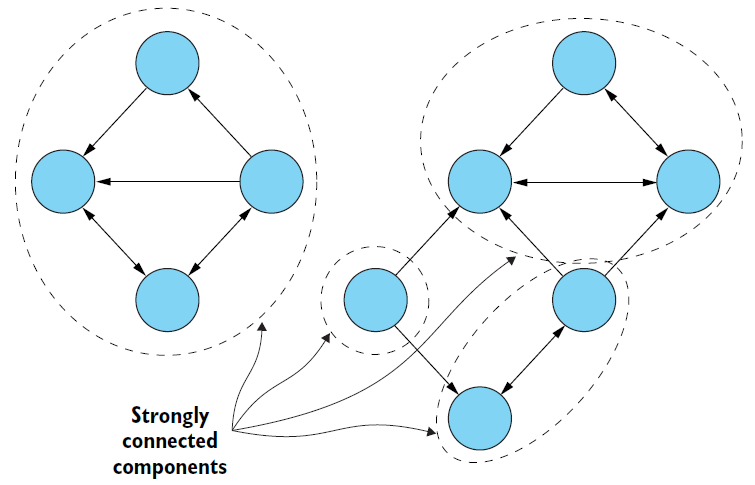
强连通组件在图论和其他领域有许多应用。例如，对于推荐引擎等应用程序，可以使用强连通的组件来分析组中的类似行为或关注的重点。

在Spark中，使用GraphOps对象的stronglyConnectedComponents()方法来计算强连通组件，它也隐式地添加到Graph对象中。执行时只需要给它指定要执行的最大迭代次数即可。

// 图的强连通组件(SCC)是一个子图，它包含可从同一子图中的每个其他顶点到达的顶点。
// 在SCC中，任何顶点都可以从任何其他顶点通过沿它们所指向的方向遍历边而到达
val wikiSCC = wikigraph.stronglyConnectedComponents(100)
wikiSCC.vertices.take(10).foreach(println)

输出内容如下：

(1210,3)
(3586,6)
(1084,6)
(1410,6)
(3456,6)
(3702,6)
(3272,6)
(3066,6)
(4038,6)
(4374,6)
(1894,6)

与上一节连通组件算法一样，由SCC算法生成的图的顶点包含了它们所属的强连通组件的最低顶点ID。该wikiSCC图包含519个强连通的组件：

// 该图中有多少个强连通组件？
println(wikiSCC.vertices.map(x => x._2).distinct.count)

输出内容如下：

最大的强连通组件是哪一个？

// 最大的强连通组件是哪一个？
wikiSCC.vertices.map(x => (x._2, x._1))
      .countByKey()
      .filter(_._2 > 1)
      .toList
      .sortWith((x, y) => x._2 > y._2)
      .foreach(println)

输出内容如下：

(6,4051)
(2488,6)
(1831,3)
(892,2)
(1950,2)
(4224,2)
(1111,2)
(2474,2)
(477,2)
(557,2)
(2160,2)
(1834,2)
(2251,2)
(1513,2)
(2142,2)
(1986,2)
(195,2)
(1976,2)
(2321,2)

最大的SCC有4051个顶点，这太多了，无法在这里显示。我们可以在几个较小的SCC中检查属于这些顶点的页面的名称。对于SCC找到的接下来的三个最大值，第一个SCC的成员是各大洲的国家名单列表：

wikiSCC.vertices.filter(x => x._2 == 2488)
      .join(articles.map(_.swap))
      .collect
      .foreach(println)

输出内容如下：

(2498,(2488,List_of_South_American_countries))
(2490,(2488,List_of_Asian_countries))
(2496,(2488,List_of_Oceanian_countries))
(2488,(2488,List_of_African_countries))
(2493,(2488,List_of_European_countries))
(2495,(2488,List_of_North_American_countries))

第二个SCC包含关于一个恒星（HD_217107）和它的两个行星的页面：

wikiSCC.vertices.filter(x => x._2 == 1831).
      join(articles.map(_.swap)).
      collect.
      foreach(println)

输出内容如下：

(1832,(1831,HD_217107_b))
(1833,(1831,HD_217107_c))
(1831,(1831,HD_217107))

第三个SCC的成员是英格兰的地区：

wikiSCC.vertices.filter(x => x._2 == 892)
      .join(articles.map(_.swap))
      .collect
      .foreach(println)

输出内容如下：

(892,(892,Chiltern_Hills))
(1262,(892,Dunstable_Downs))

小白学苑

让大数据学习更简单

GraphX内置图算法5：强连通组件