小白学苑

GraphX内置图算法4：连通组件

连通组件是图的一个子图。在这个子图中，每个顶点都可以通过子图中的边来到达另一个顶点。如果一个图只包含一个连通的组件，并且它的所有顶点都可以从其他顶点到达，那么这个图就是连通的。下面这张图中显示了具有两个连通组件的图：来自一个连通组件的顶点不能从另一个连通组件到达。

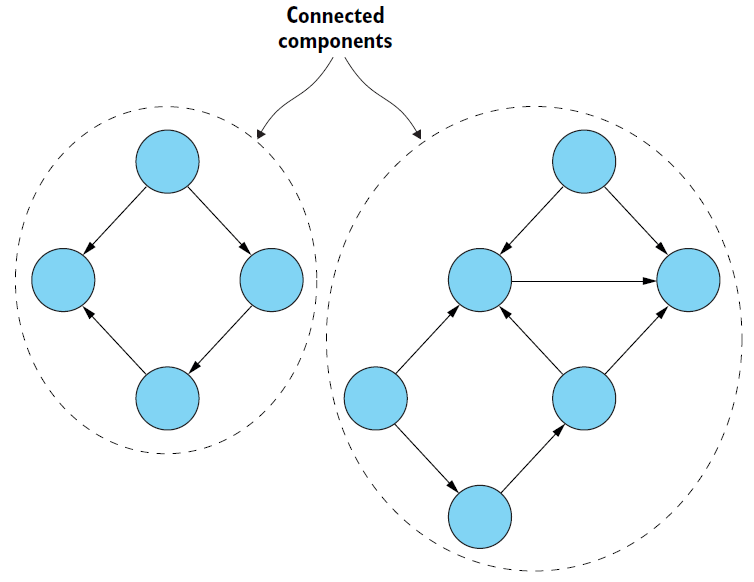
在许多情况下，寻找连通的组件是很重要的。比如，在运行其他算法之前，应该先检查此图是否是连通的，因为这可能会影响到结果并影响到结论。

要在一个GraphX图上找到连通的组件，可以调用其connectedComponents方法（隐式地从GraphOps对象中获得）。连通的组件由该连通组件中的最低顶点ID表示。下面计算Wikispeedias图中每个顶点的连通组件隶属关系。

// connectedComponents：该方法实现了连通组件算法，该算法计算每个顶点的连通组件隶属度。
// 它返回一个图形，其中每个顶点的属性是连接组件中编号最少的顶点的顶点id
val wikiCC = wikigraph.connectedComponents()
wikiCC.vertices.take(10).foreach(println)

输出内容如下所示：

(3586,0)
(1084,0)
(1410,0)
(3456,0)
(3702,0)
(3272,0)
(3066,0)
(4038,0)
(4374,0)
(1894,0)

wikiCC图的顶点的属性对象包含它们所属的连通组件的最低顶点ID。要找到这些ID的页面名称，可以再次将它们与articles RDD进行join连接：

wikiCC.vertices
      .map(x => (x._2, x._2))
      .distinct()
      .join(articles.map(_.swap))
      .collect
      .foreach(println)

输出内容如下所示：

(0,(0,%C3%81ed%C3%A1n_mac_Gabr%C3%A1in))
(1210,(1210,Directdebit))

如图中所见，Wikispeedia图有两个独立的web页面集群。第一个是由与有关的页面的顶点ID标识的，第二个是Direct Debit页面的顶点ID。

让我们看一看在每个集中群有多少页面：

wikiCC
      .vertices
      .map(x => (x._2, 1))
      .countByKey()
      .foreach(println)

输出内容如下：

(0,4589)
(1210,3)

可以看出，第二个集群只有三页，这意味着Wikispeedia具有很好的连通性。